library("tidyverse") # Regular data wrangling
library("mdatools") # Chemometrics
library("yardstick") # Additional performance metrics
library("qs") # Loading serialized files4 Chemometrics
In this section, we introduce an alternative modeling paradigm that is commonly referred as Chemometrics. According to Wikipedia,
Chemometrics is the science of extracting information from chemical systems by data-driven means. Chemometrics is inherently interdisciplinary, using methods frequently employed in core data-analytic disciplines such as multivariate statistics, applied mathematics, and computer science, in order to address problems in chemistry, biochemistry, medicine, biology and chemical engineering. In this way, it mirrors other interdisciplinary fields, such as psychometrics and econometrics.
Chemometrics has been largely employed in soil spectroscopy especially with the use of traditional preprocessing tools and Partial Least Squares Regression (PLSR). PLSR is a classic algorithm that is able do deal with the multivariate and multicolinear nature of the spectra to create robust regression models. Along with regression, many other features were built around PLSR and PCA that aid in the interpretation of models and prediction results. Therefore, this section will present and discuss these possibilities.
The choice of using classic Chemometrics tools or the ones presented in the Processing and Machine Learning sections will largely depend on the project application and familiarity. There is no perfect method so we usually recommend testing both and choosing the one that best suit your needs.
The mdatools R package is a collection of Chemometrics features that share a common “user interface”. It contains a series of features for preprocessing, exploring, modeling, and interpreting multivariate spectral data.
The mdatools framework is presented in Kucheryavskiy (2020). For a full documentation of the available features, please visit https://mdatools.com/docs/index.html.
A list of all required packages for this section is provided in the following code chunk:
4.1 Preparation of files
Instead of using the train.csv and test.csv files from the Machine Learning section, we are going to preprocess and model the same spectral data using a different set of tools. For this, we are going to use the same Neospectra database that is part of the Open Soil Spectral Library (OSSL).
## Internet configuration for downloading big datasets
options(timeout = 10000)
## Reading serialized files
neospectra.soil <- qread_url("https://storage.googleapis.com/soilspec4gg-public/neospectra_soillab_v1.2.qs")
dim(neospectra.soil)[1] 2106 24neospectra.site <- qread_url("https://storage.googleapis.com/soilspec4gg-public/neospectra_soilsite_v1.2.qs")
dim(neospectra.site)[1] 2106 32neospectra.nir <- qread_url("https://storage.googleapis.com/soilspec4gg-public/neospectra_nir_v1.2.qs")
dim(neospectra.nir)[1] 8151 615From the original files, we can now select only the relevant data for our modeling.
# Selecting relevant site data
neospectra.site <- neospectra.site %>%
select(id.sample_local_c, location.country_iso.3166_txt)
# Selecting relevant soil data
neospectra.soil <- neospectra.soil %>%
select(id.sample_local_c, oc_usda.c729_w.pct)
# Selecting relevant NIR data and taking average across repeats
neospectra.nir <- neospectra.nir %>%
select(id.sample_local_c, starts_with("scan_nir")) %>%
group_by(id.sample_local_c) %>%
summarise_all(mean, .group = "drop")
# Renaming spectral columns headers to numeric integers
neospectra.nir %>%
select(starts_with("scan_nir")) %>%
names() %>%
head()[1] "scan_nir.1350_ref" "scan_nir.1352_ref" "scan_nir.1354_ref"
[4] "scan_nir.1356_ref" "scan_nir.1358_ref" "scan_nir.1360_ref"old.names <- neospectra.nir %>%
select(starts_with("scan_nir")) %>%
names()
new.names <- gsub("scan_nir.|_ref", "", old.names)
neospectra.nir <- neospectra.nir %>%
rename_with(~new.names, all_of(old.names))
spectral.column.names <- new.names
head(spectral.column.names)[1] "1350" "1352" "1354" "1356" "1358" "1360"tail(spectral.column.names)[1] "2540" "2542" "2544" "2546" "2548" "2550"Lastly, we just make sure to have all data prepared and complete.
# Joining data
neospectra <- left_join(neospectra.site,
neospectra.soil,
by = "id.sample_local_c") %>%
left_join(., neospectra.nir, by = "id.sample_local_c")
# Filtering out samples without SOC values
neospectra <- neospectra %>%
filter(!is.na(oc_usda.c729_w.pct))A subset of the imported spectra can be visualized below.
# Spectral visualization
set.seed(1993)
neospectra %>%
sample_n(100) %>%
pivot_longer(any_of(spectral.column.names),
names_to = "wavelength",
values_to = "reflectance") %>%
mutate(wavelength = as.numeric(wavelength),
reflectance = as.numeric(reflectance)) %>%
ggplot(data = .) +
geom_line(aes(x = wavelength, y = reflectance, group = id.sample_local_c),
alpha = 0.25, linewidth = 0.25) +
theme_light()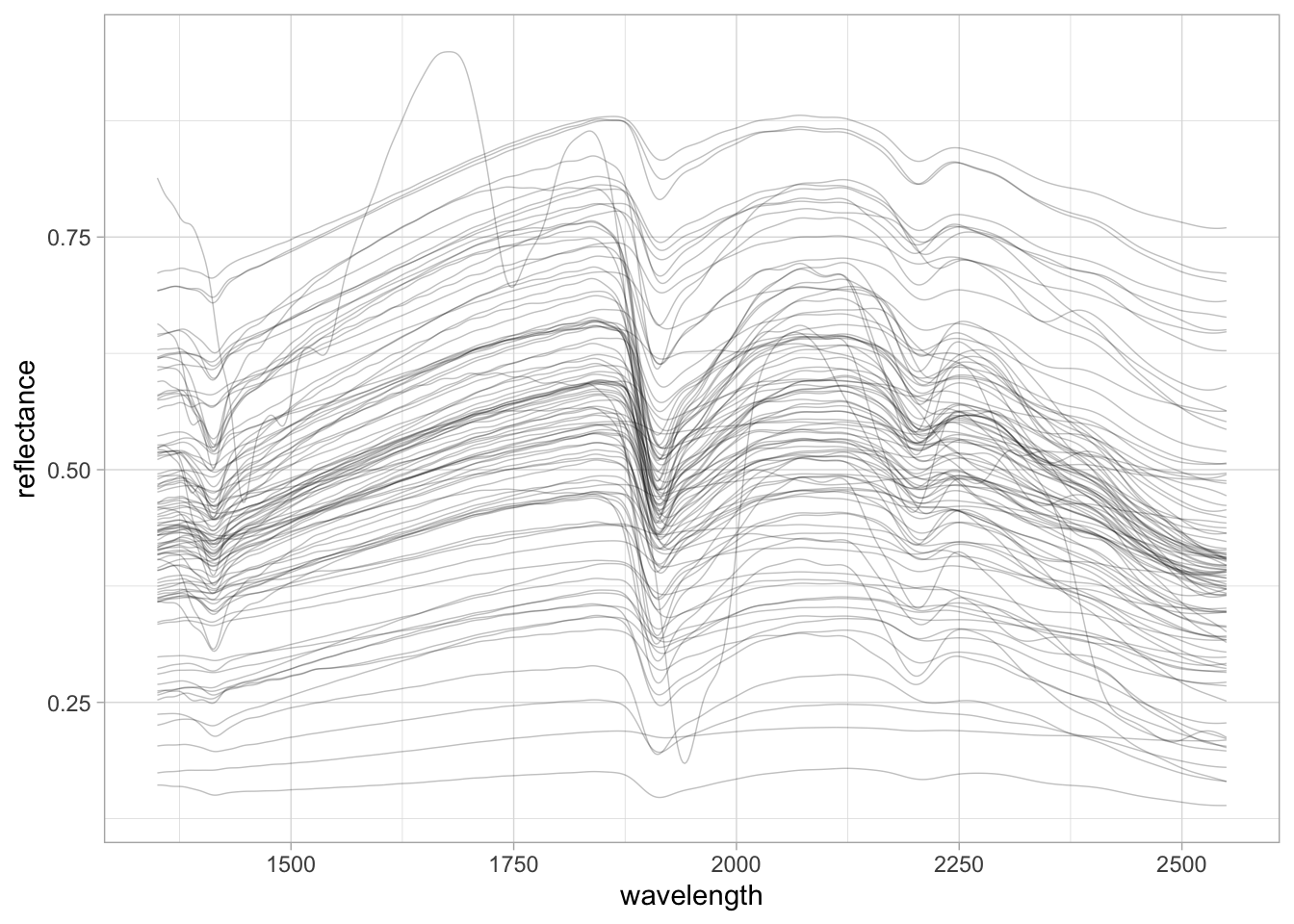
4.2 Chemometric modeling
To start with chemometrics, the mdatools offer a series of built-in function for preprocessing spectra. We are going to use the Standard Normal Variate function.
# Preprocessing with SNV
neospectra.snv <- neospectra %>%
select(all_of(spectral.column.names)) %>%
as.matrix() %>%
prep.snv(.) %>%
as_tibble() %>%
bind_cols({neospectra %>%
select(-all_of(spectral.column.names))}, .)
# Visualization
set.seed(1993)
neospectra.snv %>%
sample_n(100) %>%
pivot_longer(any_of(spectral.column.names),
names_to = "wavelength",
values_to = "reflectance") %>%
mutate(wavelength = as.numeric(wavelength),
reflectance = as.numeric(reflectance)) %>%
ggplot(data = .) +
geom_line(aes(x = wavelength, y = reflectance, group = id.sample_local_c),
alpha = 0.25, linewidth = 0.25) +
theme_light()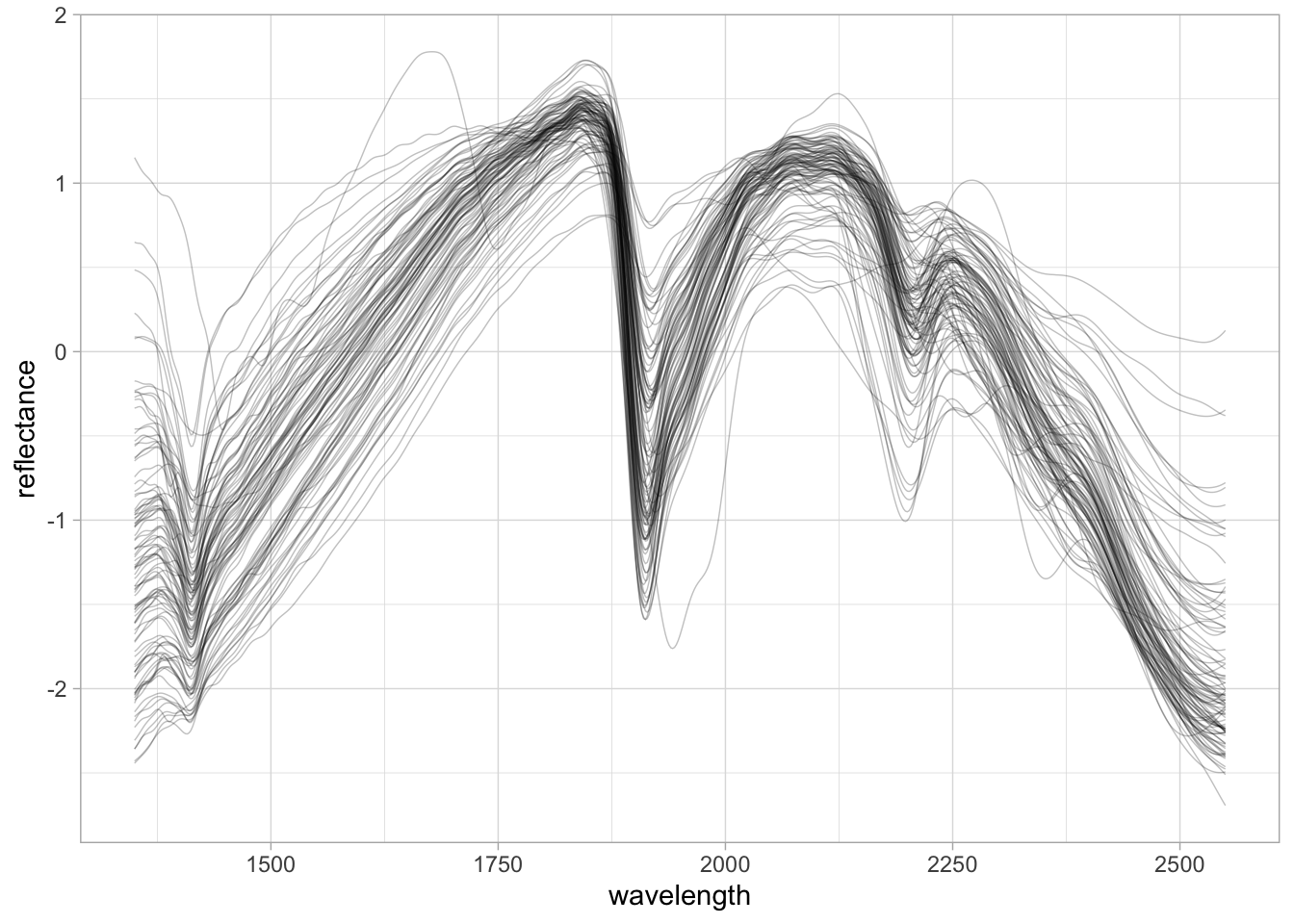
Before model calibration, we are going to split the dataset into train and test sets. We use the same split rule employed in the Machine Learning section.
# Preparing train split, separating predictors and outcome, and applying log1p
neospectra.train <- neospectra.snv %>%
filter(location.country_iso.3166_txt == "USA")
neospectra.train.predictors <- neospectra.train %>%
select(all_of(spectral.column.names))
neospectra.train.outcome <- neospectra.train %>%
select(oc_usda.c729_w.pct) %>%
mutate(oc_usda.c729_w.pct = log1p(oc_usda.c729_w.pct))
# Preparing test split, separating predictors and outcome, and applying log1p
neospectra.test <- neospectra.snv %>%
filter(location.country_iso.3166_txt != "USA")
neospectra.test.predictors <- neospectra.test %>%
select(all_of(spectral.column.names))
neospectra.test.outcome <- neospectra.test %>%
select(oc_usda.c729_w.pct) %>%
mutate(oc_usda.c729_w.pct = log1p(oc_usda.c729_w.pct))Now we just feed the preprocessed spectra into the PLSR algorithm.
PLSR in this case, will compress the spectra into several orthogonal features that both maximize the variance in the spectra and the soil property of interest, in this case, SOC. The resulting scores from these latent factors are feed in a multivariate linear regression model.
If you want to learn more about PLSR and PCA, the mdatools documentation offers a good explanation. Similarly, take a look at this awesome chapter from All Models Are Wrong: Concepts of Statistical Learning.
We are going to test up to 20 factors (ncomp = 20), run 10-fold cross-validation for the train data (cv = 10), center and scale the spectra before compression (which are performed locally, i.e., independently for each fold [center = TRUE, scale = TRUE, cv.scope = 'local']), and use a data driven method ("ddmoments") to estimate critical limits for the extreme and outlier samples. The model is named “SOC prediction model”.
We can fit a PLSR by passing the train and test samples together in the call…
set.seed(1993)
pls.model.soc <- pls(x = neospectra.train.predictors,
y = neospectra.train.outcome,
ncomp = 20,
x.test = neospectra.test.predictors,
y.test = neospectra.test.outcome,
center = TRUE, scale = TRUE,
cv = 10, lim.type = "ddmoments", cv.scope = 'local',
info = "SOC prediction model")Or run separately.
# Alternatively
set.seed(1993)
pls.model.soc.calibration <- pls(x = neospectra.train.predictors,
y = neospectra.train.outcome,
ncomp = 20,
center = TRUE, scale = TRUE,
cv = 10, lim.type = "ddmoments", cv.scope = 'local',
info = "SOC prediction model")
pls.model.soc.predictions <- predict(pls.model.soc.calibration,
x = neospectra.test.predictors,
y = neospectra.test.outcome, cv = F)From these model fits, we can get a summary of the model.
# Get an overview of performance
summary(pls.model.soc)
PLS model (class pls) summary
-------------------------------
Info: SOC prediction model
Number of selected components: 17
Cross-validation: random with 10 segments
Response variable: oc_usda.c729_w.pct
X cumexpvar Y cumexpvar R2 RMSE Slope Bias RPD
Cal 99.89127 74.54372 0.745 0.286 0.745 0.0000 1.98
Cv NA NA 0.728 0.296 0.739 -0.0010 1.92
Test 99.85834 67.54793 0.370 0.295 0.605 -0.1258 1.40You can see that the number of selected components is 17, which was automatically chosen from 10CV results.
Let’s plot the models. We will explore in detail the visualization features soon.
# Visualize representation limits, model coefficient, performance and fit
# Remove legend for proper visualization
plot(pls.model.soc, show.legend = T)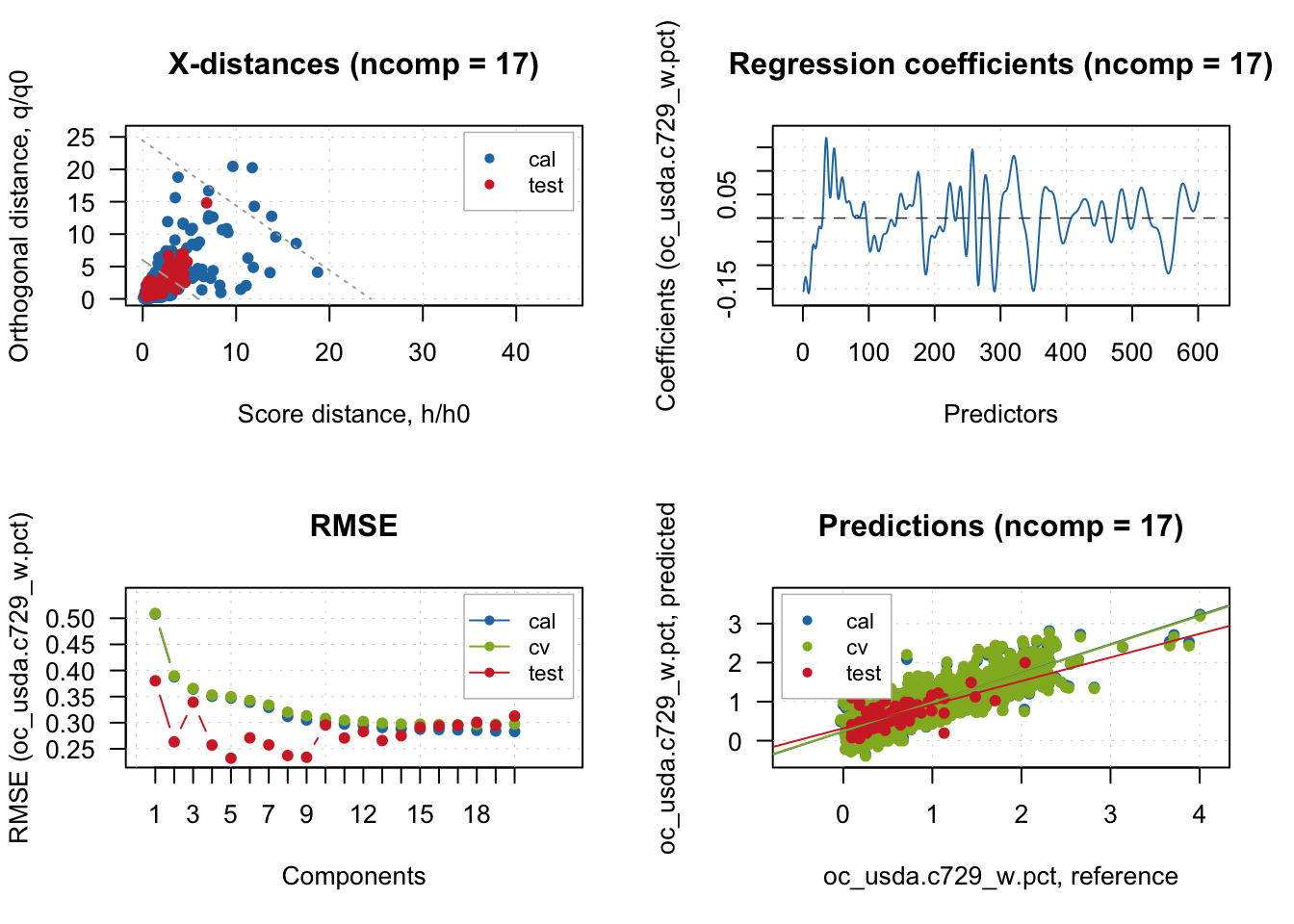
There is big mismatch between CV and test performance, and this happened likely due to the geographical difference of the samples. Let’s set the number of comps that worked best for test samples.
# The performance is more consistent across train, cv, and test with 5 comps
pls.model.soc <- selectCompNum(pls.model.soc, 5)
summary(pls.model.soc)
PLS model (class pls) summary
-------------------------------
Info: SOC prediction model
Number of selected components: 5
Cross-validation: random with 10 segments
Response variable: oc_usda.c729_w.pct
X cumexpvar Y cumexpvar R2 RMSE Slope Bias RPD
Cal 97.38915 62.53123 0.625 0.347 0.625 0.0000 1.63
Cv NA NA 0.620 0.350 0.623 -0.0008 1.62
Test 97.08588 79.92043 0.610 0.232 0.534 0.0378 1.63plot(pls.model.soc, show.legend = F)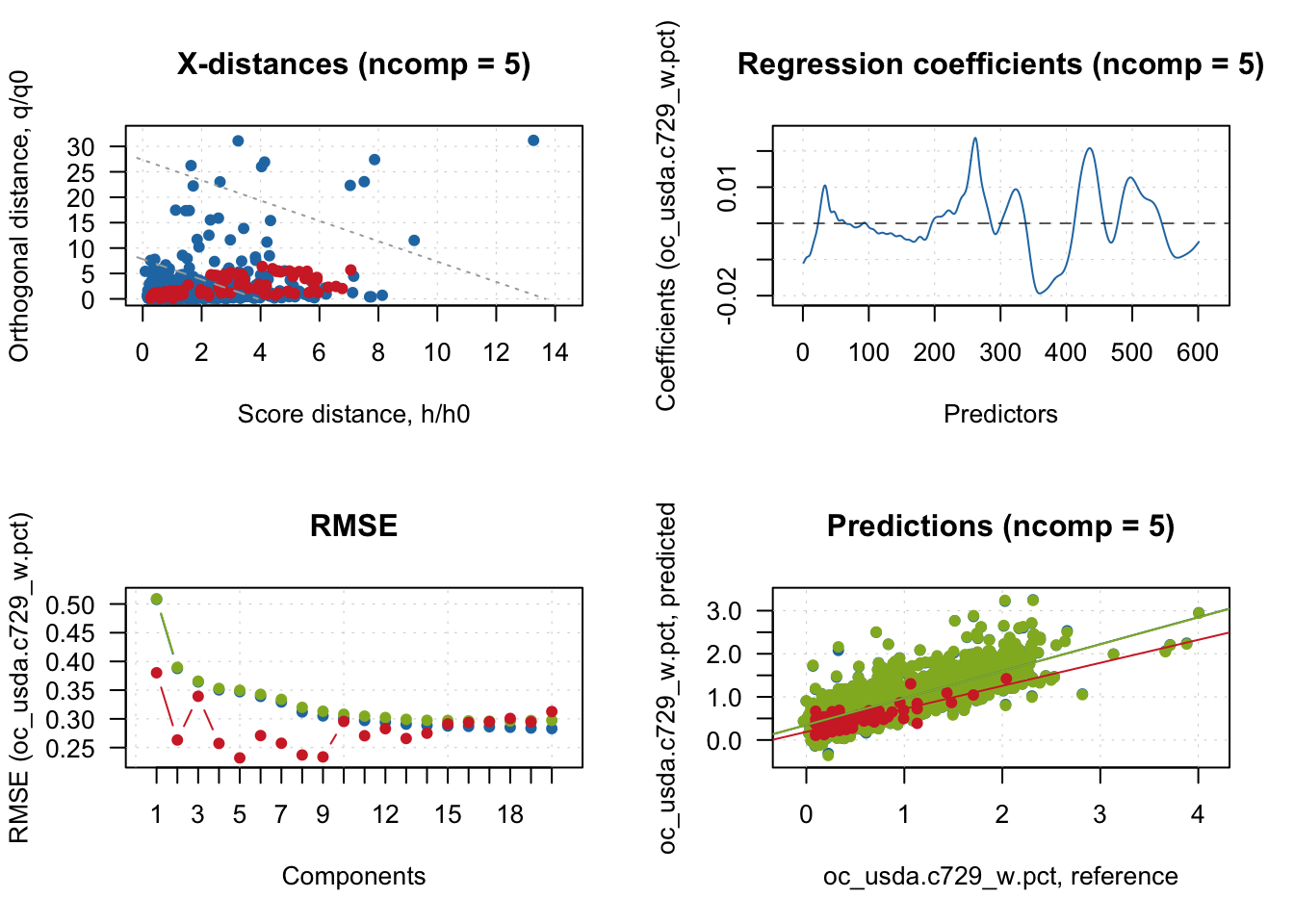
5 Model and predictions interpretation
We can start the interpretation by looking at the observations classification based on the spectral dissimilarity. For this, mdatools use both the Q statistics and Hotelling \(T^2\) as distance metrics for classifying samples into regular, extreme or outlier.
The Q statistics, known as orthogonal distance in mdatools, measures the remaining spectral variance that is not accounted during spectral compression and is not used by the models. Therefore, observations with unique features not well represented by PLSR are flagged. On the other hand, the Hotelling \(T^2\) focus on the mean deviation of observation values (scores) produced by the retained factors used in the models, with very distinct samples being flagged. Therefore, these two complimentary methods are able to detect potential observations that are underrepresented by the PLSR model. The classification is based on critical limits that are calculated from the calibration set, and mdatools currently make possible to use four different methods. By default, it uses the data driven moments (lim.type = "ddmoments") developed by the author.
Let’s see the classification and plot it with the model residuals. We can see that for the test set, several observations were flagged as potential extreme observations, with no spectral outlier detected.
# Categorization
outlier.detection <- categorize(pls.model.soc.calibration,
pls.model.soc.predictions,
ncomp = 5)
head(outlier.detection)[1] regular regular regular regular extreme regular
Levels: regular extreme outlierplotResiduals(pls.model.soc.predictions,
cgroup = outlier.detection,
ncomp = 5)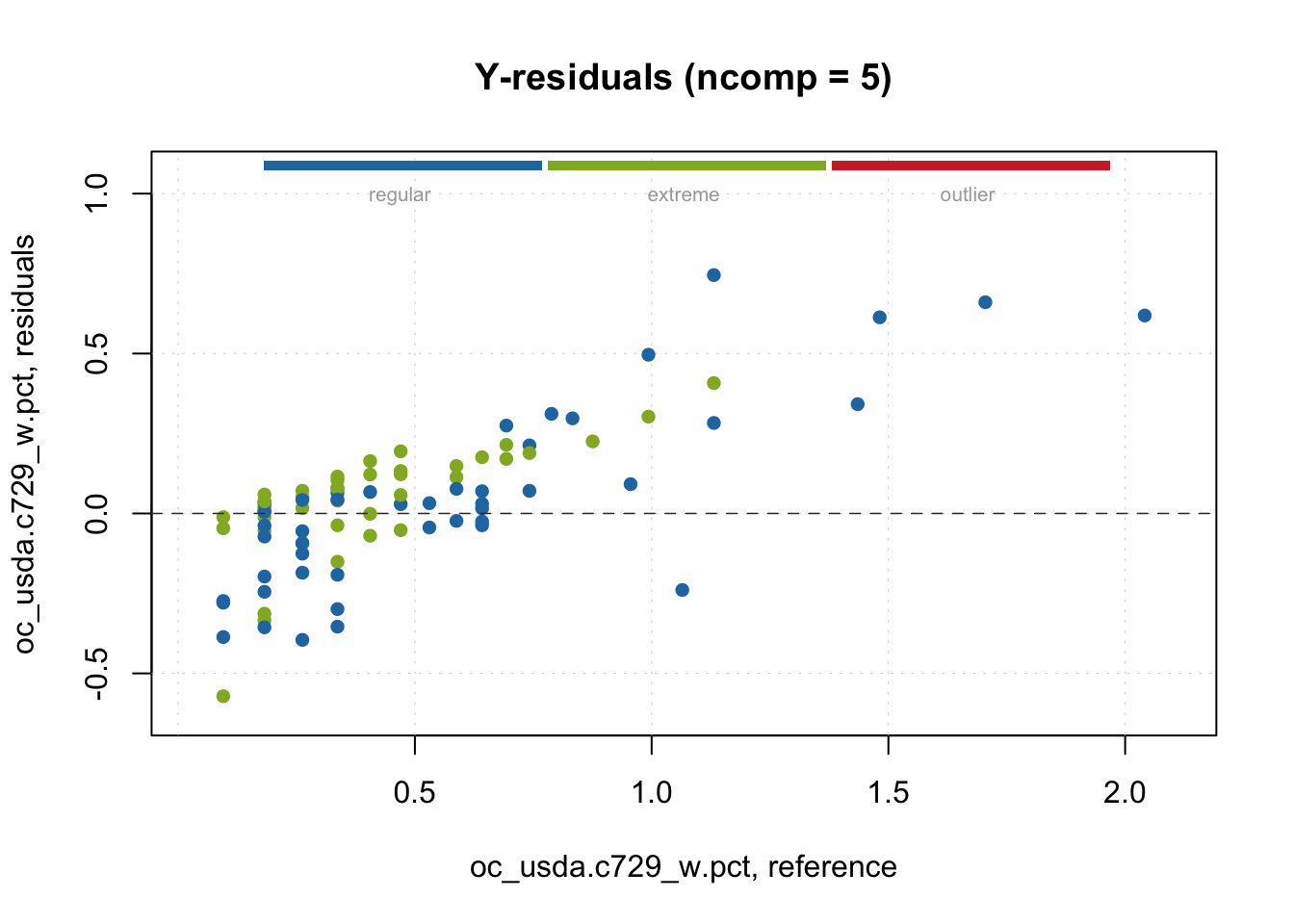
We can further explore the PLSR model with additional built-in plot functions, for example, exploring in detail the model performance across the range of components tested, for all data splits.
plotRMSE(pls.model.soc, show.labels = TRUE)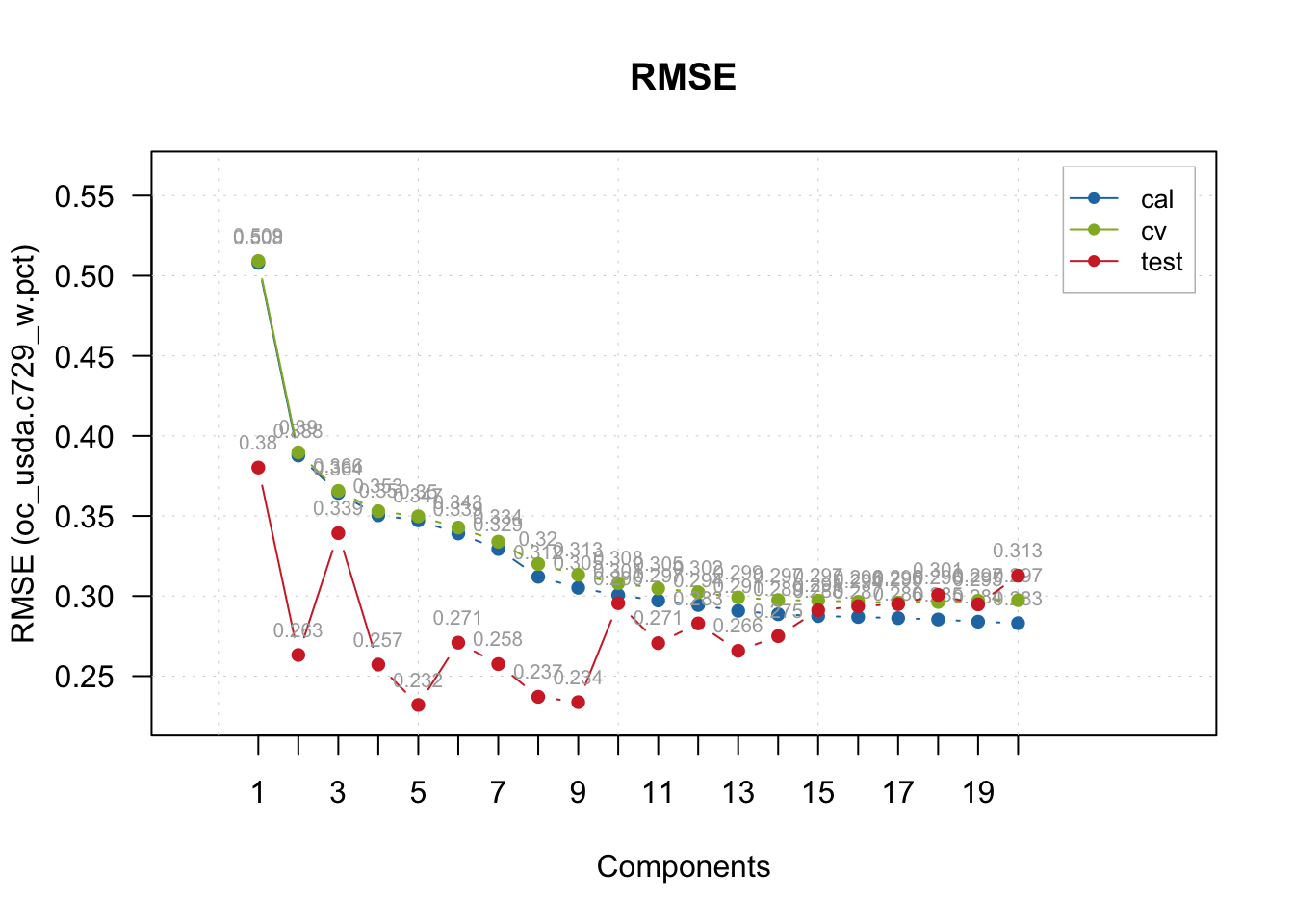
With the predictions made, we can run a classic observed vs predicted scatterplot.
# Predictions scatterplot
plotPredictions(pls.model.soc, show.line = T, pch = 20, cex = 0.25)
abline(a=0, b=1)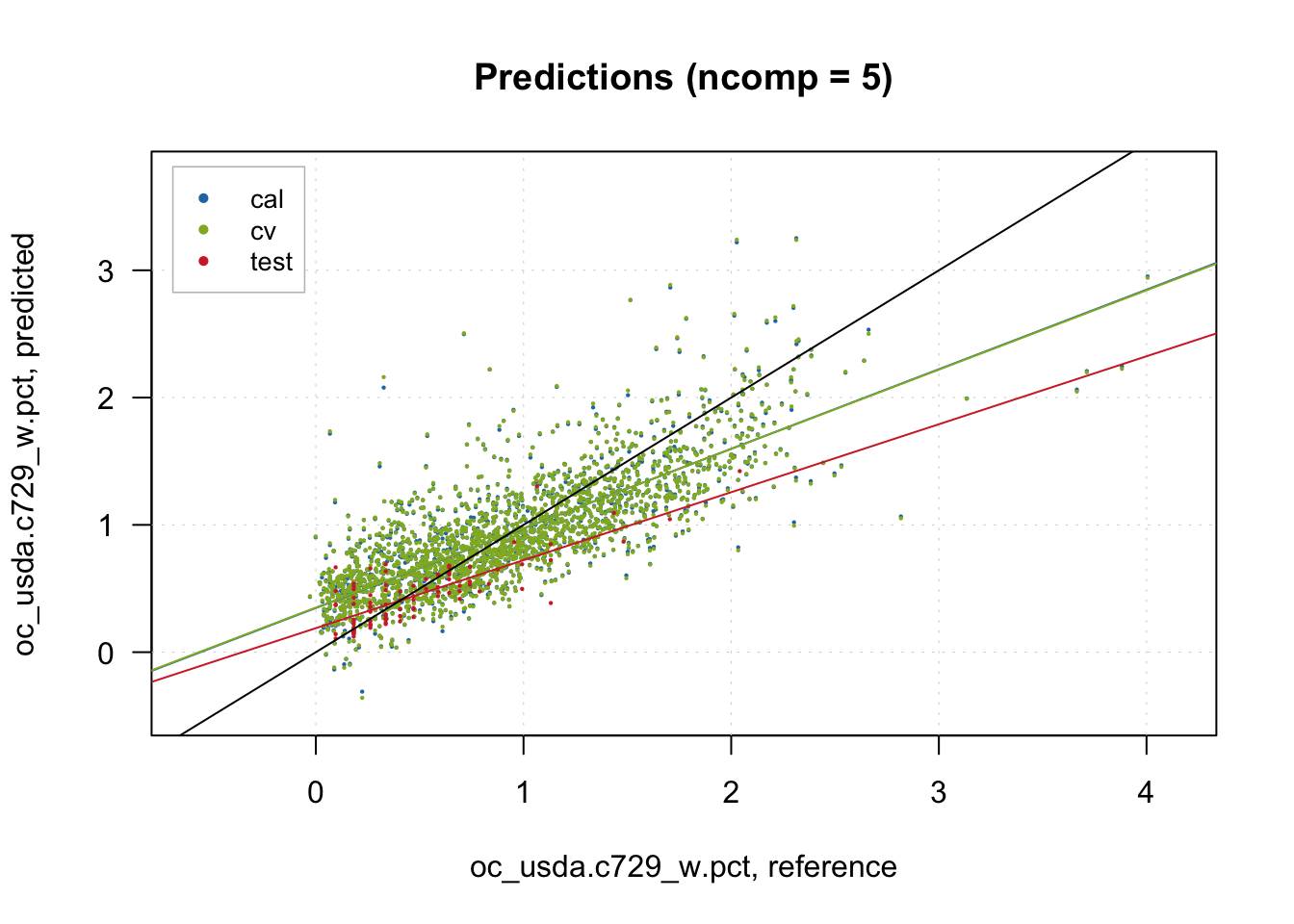
# plotPredictions(pls.model.soc.predictions, show.line = T, pch = 20, cex = 0.25)
# abline(a=0, b=1)And inspect the residuals…
# Inspection plot for outcome residual
plotYResiduals(pls.model.soc, cex = 0.5, show.label = TRUE)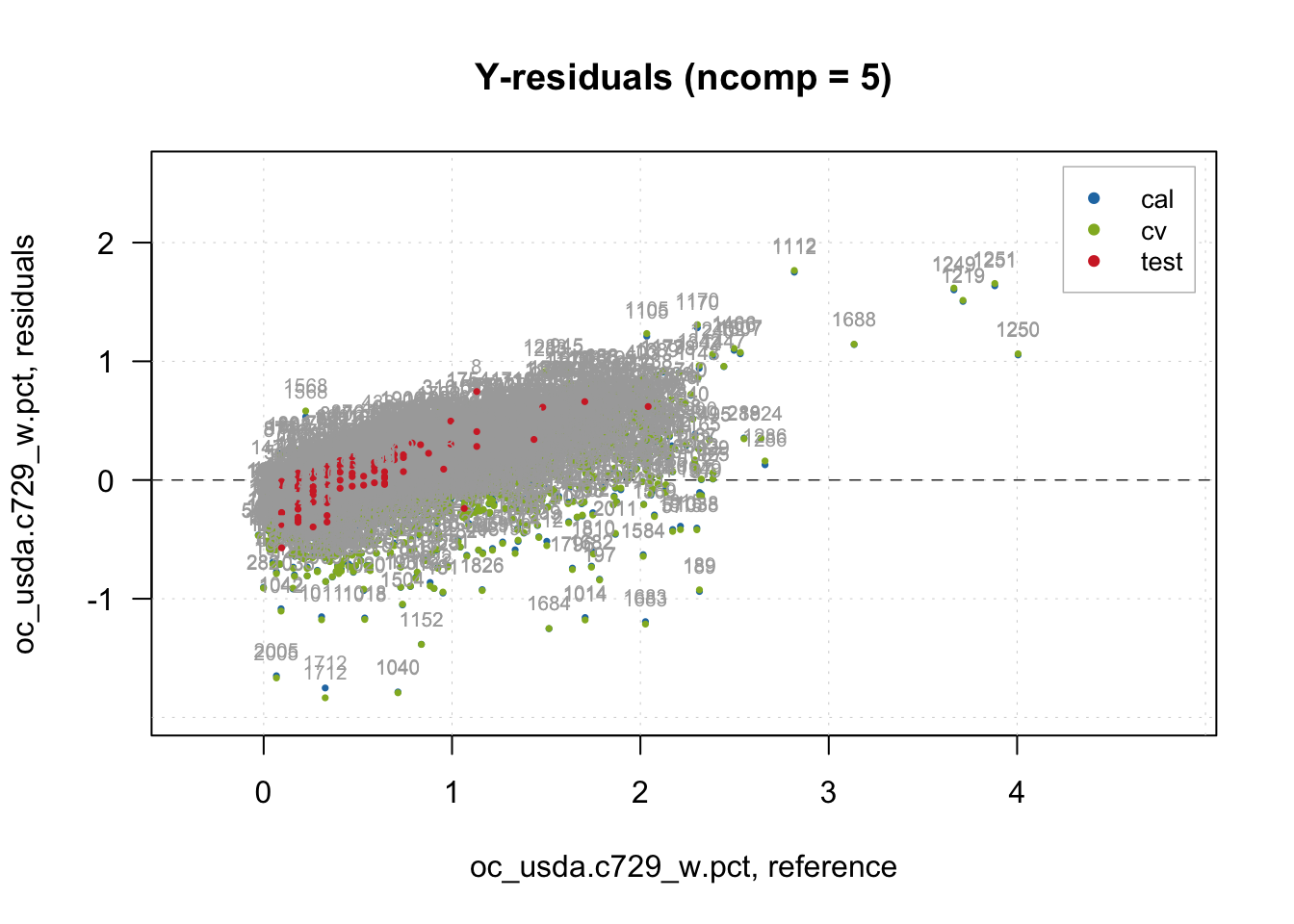
Another common visualization that aids the interpretation of models is the variable importance. For PLSR, the Variable Importance to Projection (VIP) is routinely employed.
# Variable influence on projection (VIP) scores
plotVIPScores(pls.model.soc)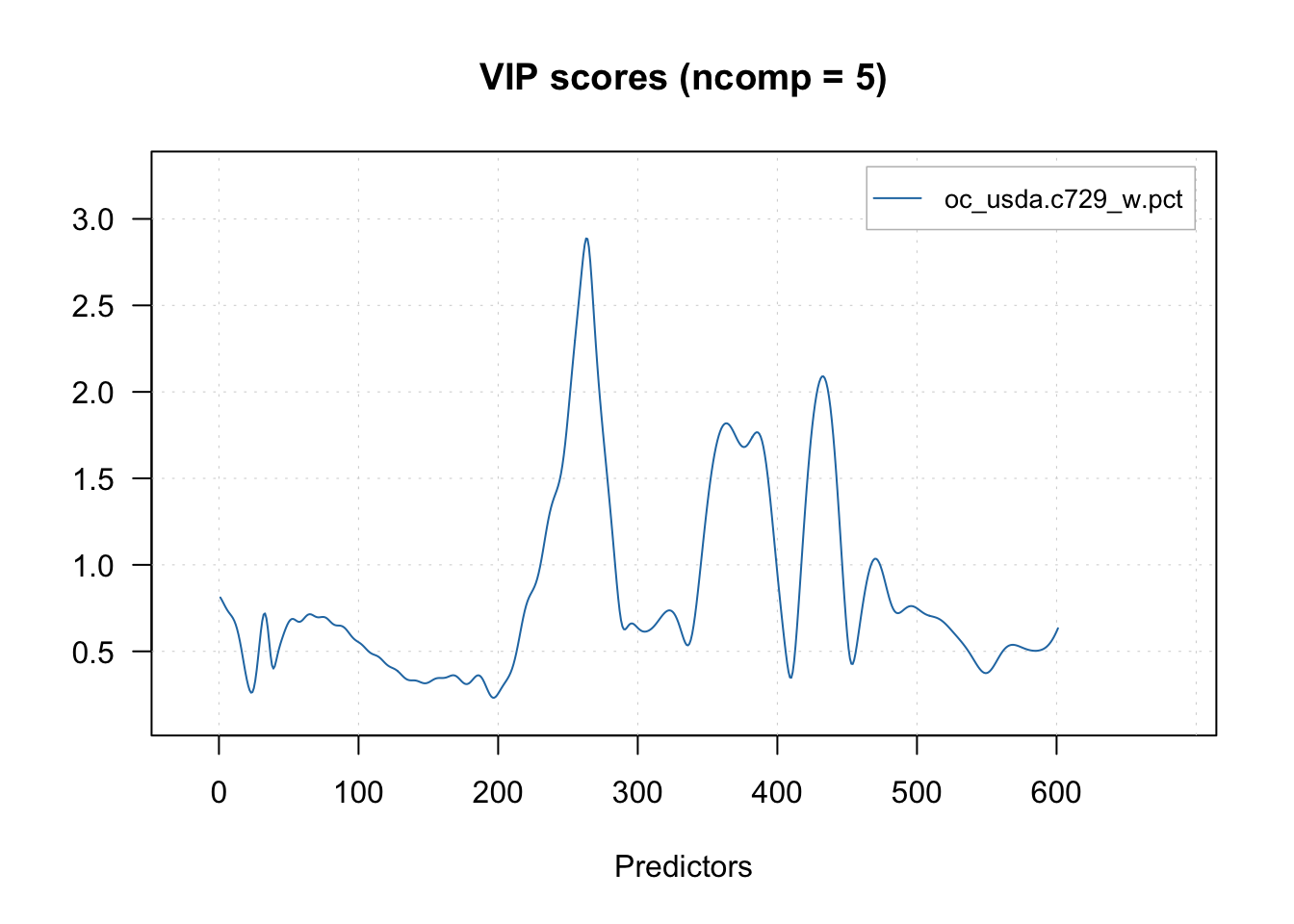
vip = vipscores(pls.model.soc, ncomp = 5)
head(vip) oc_usda.c729_w.pct
1350 0.8113615
1352 0.7976495
1354 0.7823705
1356 0.7666420
1358 0.7516056
1360 0.7379479There are many other plot functions for interpreting the PLSR model.
For example, how much of the original spectral variance (X variables) was retained by 5 components/factors? Around 97% for both train and test sets.
# Cumulative variance retained from predictors (spectra)
plotXCumVariance(pls.model.soc, type = 'h', show.labels = TRUE, legend.position = 'bottomright')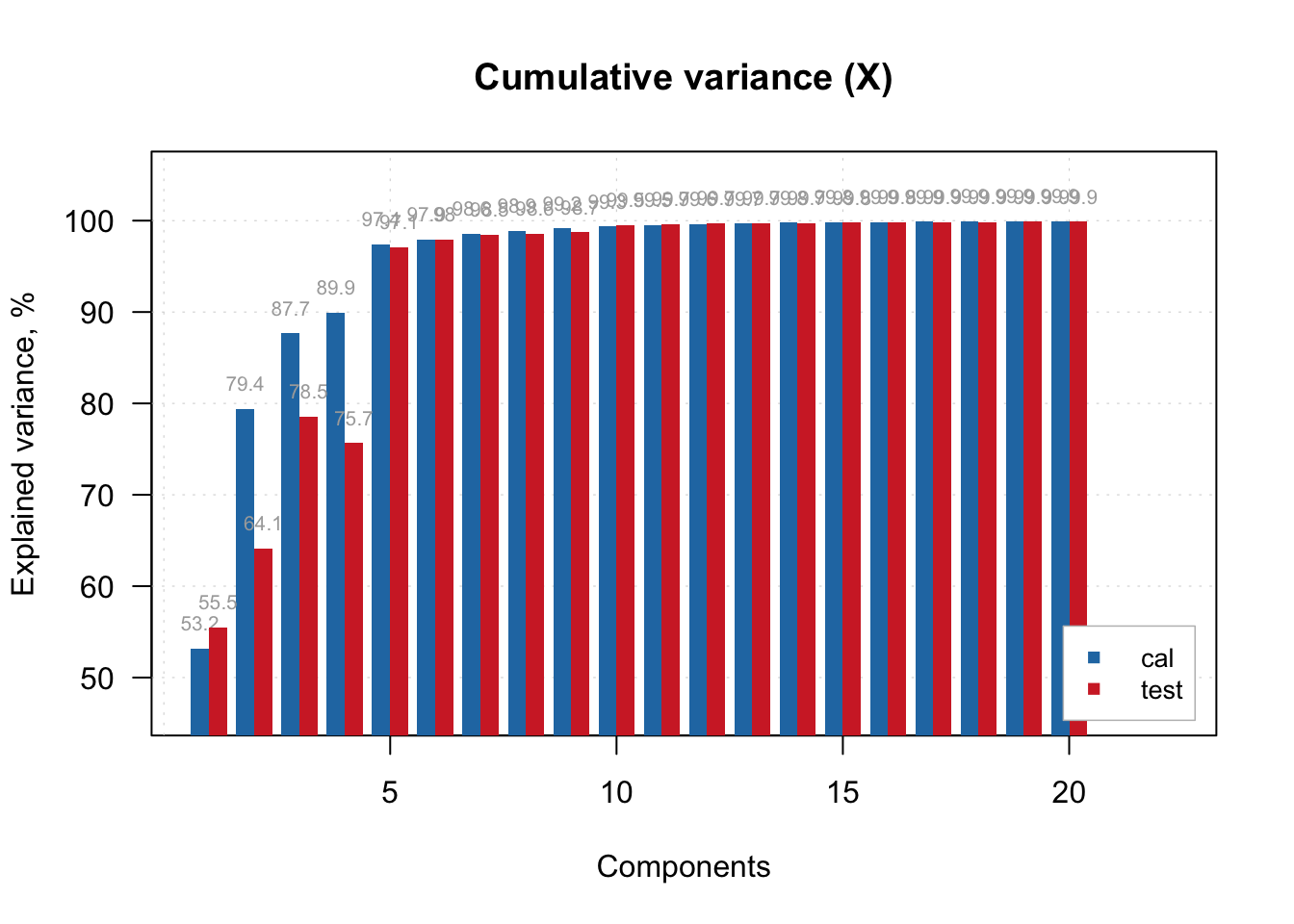
As the PLSR try to maximize both the X (predictors) and Y (single or multiple outcome) original variance during compression, how much of the outcome variance was retained by the 5 components/factors? About 40% in the train and 90% in the test samples.
# Cumulative variance retained from outcome
plotYCumVariance(pls.model.soc, type = 'b', show.labels = TRUE, legend.position = 'bottomright')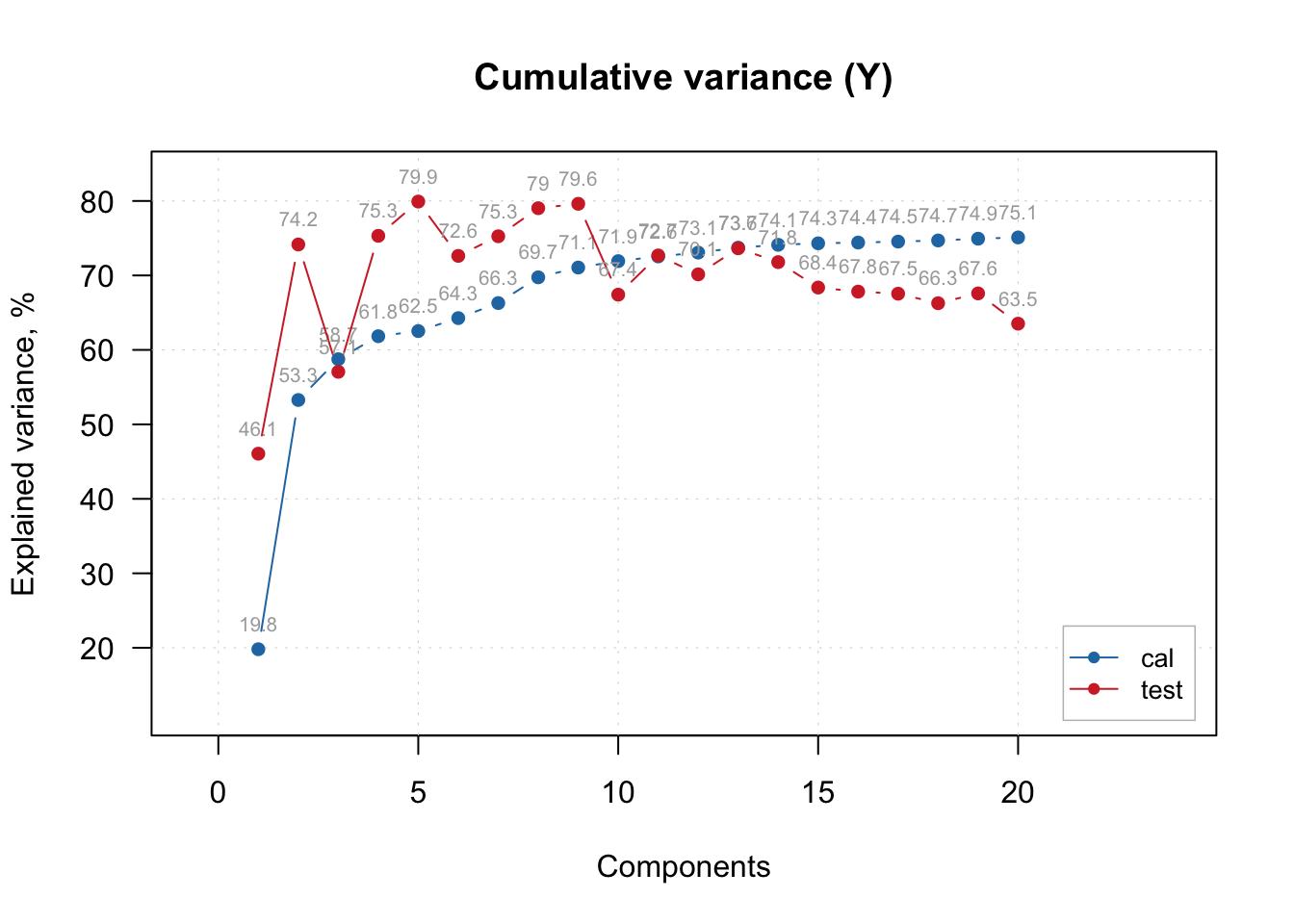
And visualize the scores of the latent factors produced. In this case, we are plotting the first 3 factors.
# Scores plots for compressed spectra ()
plotXScores(pls.model.soc, comp = c(1, 2), show.legend = T, cex = 0.5, legend.position = 'topleft')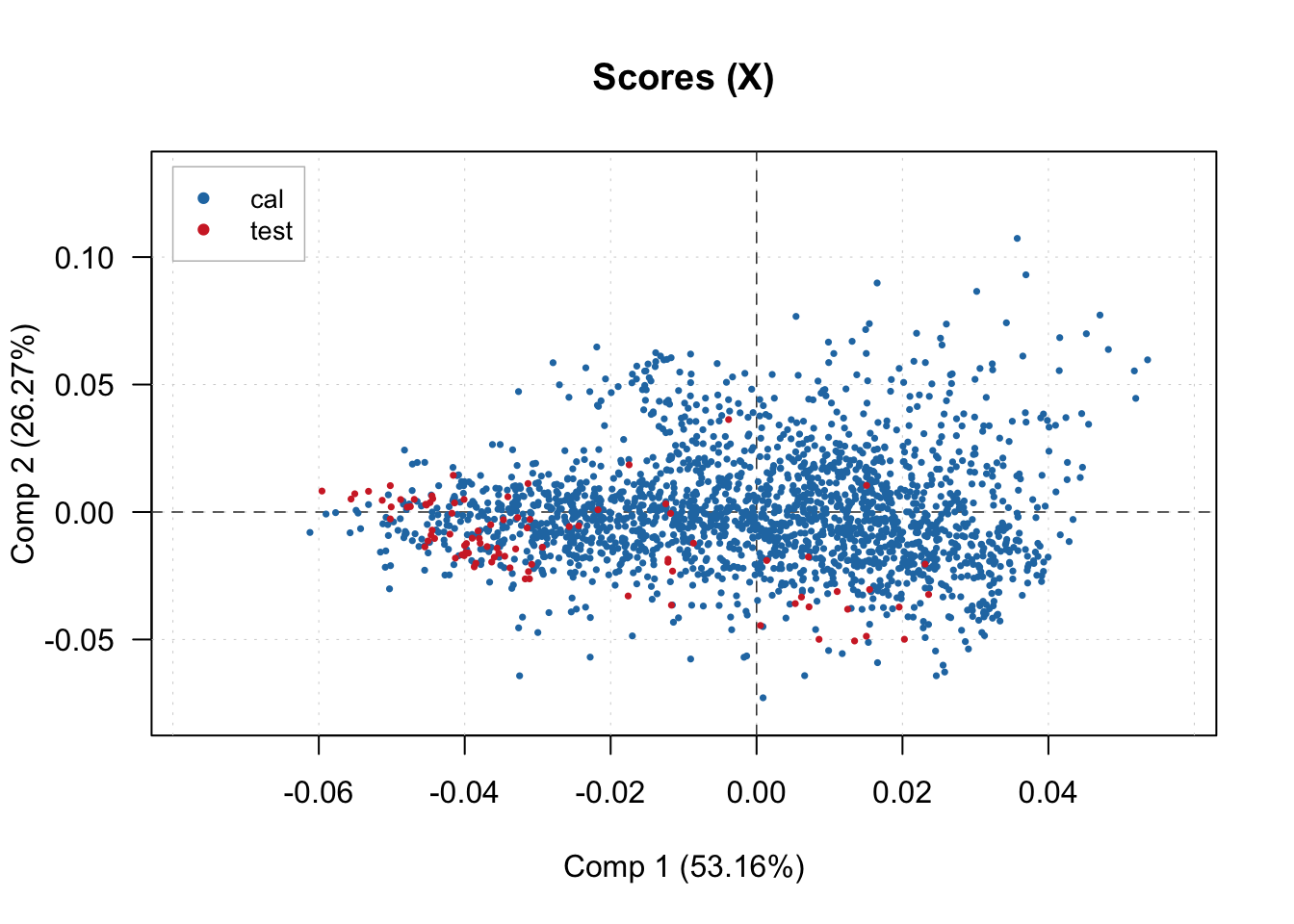
plotXScores(pls.model.soc, comp = c(1, 3), show.legend = T, cex = 0.5, legend.position = 'bottomright')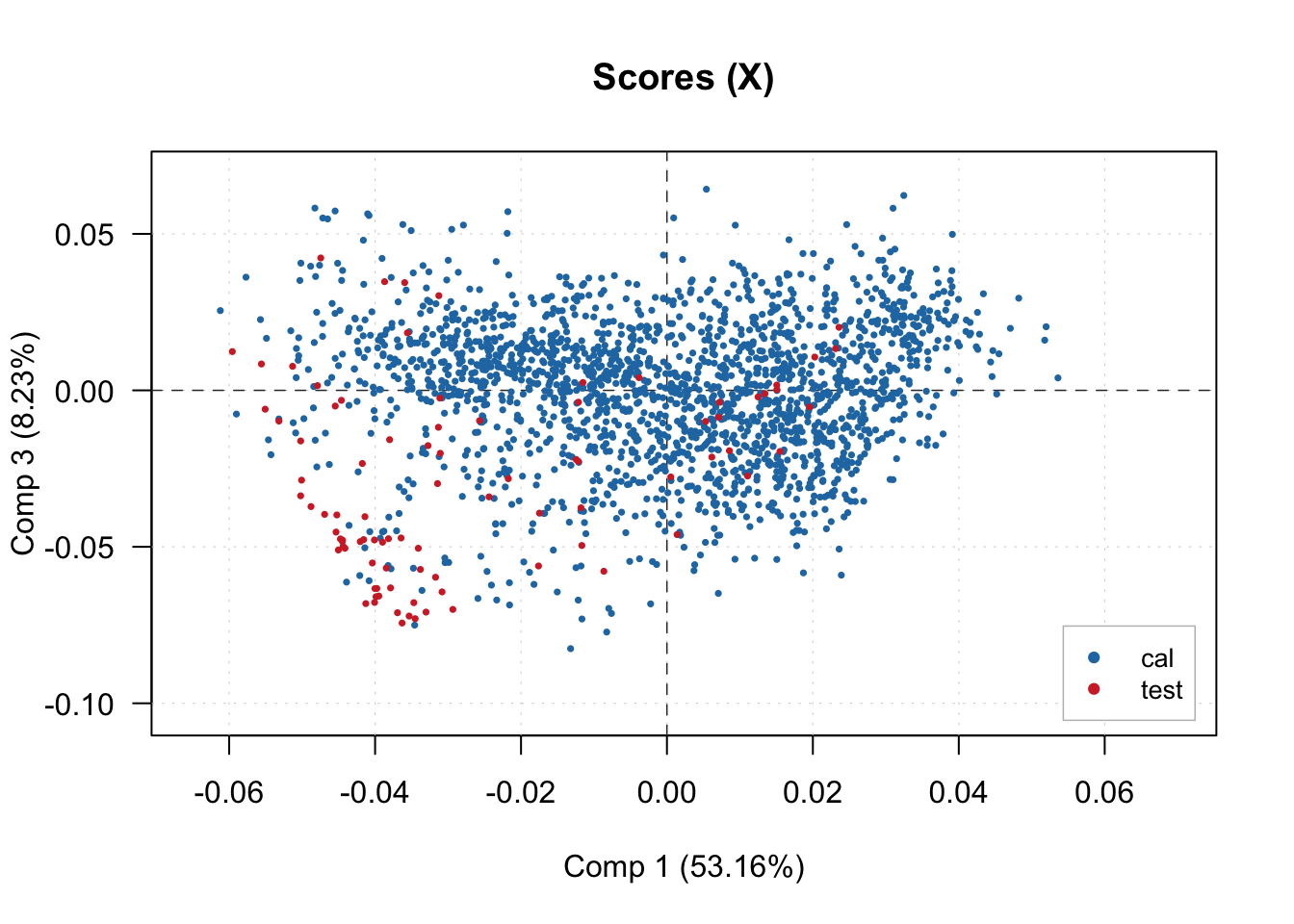
During spectra compression, we can visualize the estimated loadings for the first 5 components across the original spectrum.
# Inspection plot for outcome residual
plotXLoadings(pls.model.soc, comp = c(1, 2, 3, 4, 5), type = 'l')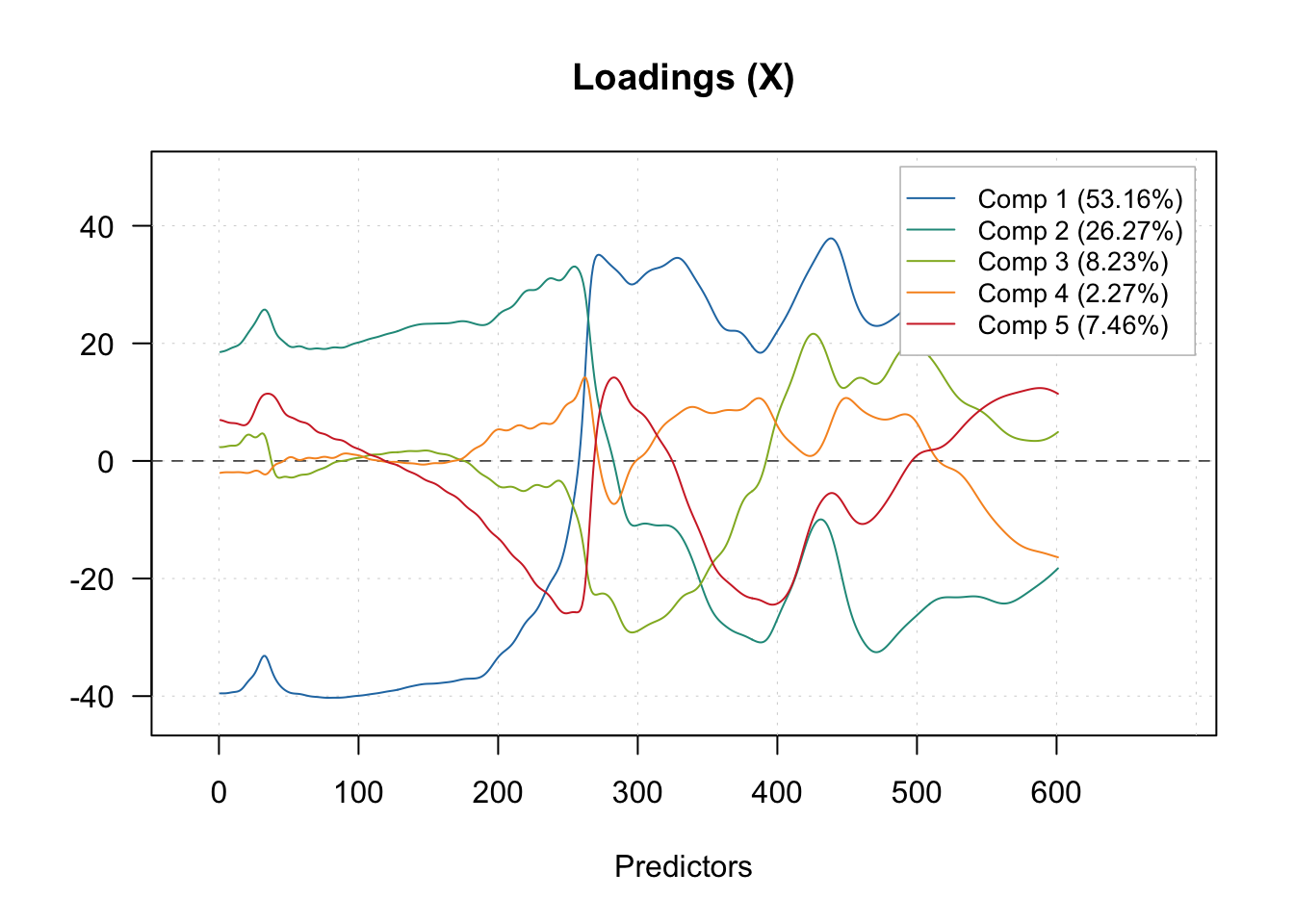
Lastly, we can explore all the internal information retained in the pls and plsres objects produced by the mdatools.
# Exploring internal info from model object
pls.model.soc$T2lim Comp 1 Comp 2 Comp 3 Comp 4 Comp 5 Comp 6
Extremes limits 3.905426 7.810852 9.483023 15.621703 19.52713 35.930956
Outliers limits 13.665454 27.330908 29.945907 54.661815 68.32727 146.435595
Mean 0.999504 1.999008 2.998512 3.998016 4.99752 5.997024
DoF 2.000000 2.000000 3.000000 2.000000 2.00000 1.000000
Comp 7 Comp 8 Comp 9 Comp 10 Comp 11 Comp 12
Extremes limits 41.919448 47.907941 53.896433 59.88493 65.87342 71.86191
Outliers limits 170.841528 195.247461 219.653393 244.05933 268.46526 292.87119
Mean 6.996528 7.996032 8.995536 9.99504 10.99454 11.99405
DoF 1.000000 1.000000 1.000000 1.00000 1.00000 1.00000
Comp 13 Comp 14 Comp 15 Comp 16 Comp 17 Comp 18
Extremes limits 77.85040 83.83890 89.82739 95.81588 101.80437 107.79287
Outliers limits 317.27712 341.68306 366.08899 390.49492 414.90085 439.30679
Mean 12.99355 13.99306 14.99256 15.99206 16.99157 17.99107
DoF 1.00000 1.00000 1.00000 1.00000 1.00000 1.00000
Comp 19 Comp 20
Extremes limits 113.78136 119.76985
Outliers limits 463.71272 488.11865
Mean 18.99058 19.99008
DoF 1.00000 1.00000
attr(,"name")
[1] "Critical limits for score distances (T2)"
attr(,"alpha")
[1] 0.05
attr(,"gamma")
[1] 0.01
attr(,"lim.type")
[1] "ddmoments"pls.model.soc$Qlim Comp 1 Comp 2 Comp 3 Comp 4 Comp 5 Comp 6
Extremes limits 2198.6340 965.6145 703.07621 472.63657 122.56192 74.60566
Outliers limits 7693.2282 3378.7763 2220.20501 1653.80002 428.85573 304.05325
Mean 281.3449 123.5634 74.10374 60.48023 15.68345 12.45199
DoF 1.0000 1.0000 1.00000 1.00000 1.00000 1.00000
Comp 7 Comp 8 Comp 9 Comp 10 Comp 11 Comp 12
Extremes limits 50.668028 39.015899 30.257438 23.62243 17.206518 13.497755
Outliers limits 206.496119 159.008195 123.313337 96.27254 70.124678 55.009721
Mean 8.456702 6.511913 5.050091 3.94268 2.871838 2.252831
DoF 1.000000 1.000000 1.000000 1.00000 1.000000 1.000000
Comp 13 Comp 14 Comp 15 Comp 16 Comp 17 Comp 18
Extremes limits 11.302109 8.559007 6.771172 5.0085256 3.9132139 3.3192646
Outliers limits 46.061426 34.881990 27.595720 20.4121046 15.9481929 13.5275694
Mean 1.886368 1.428533 1.130136 0.8359435 0.6531314 0.5539989
DoF 1.000000 1.000000 1.000000 1.0000000 1.0000000 1.0000000
Comp 19 Comp 20
Extremes limits 2.9627742 2.5821449
Outliers limits 12.0747026 10.5234585
Mean 0.4944992 0.4309706
DoF 1.0000000 1.0000000
attr(,"name")
[1] "Critical limits for orthogonal distances (Q)"
attr(,"alpha")
[1] 0.05
attr(,"gamma")
[1] 0.01
attr(,"lim.type")
[1] "ddmoments"pls.model.soc$res$cal
PLS results (class plsres)
Call:
plsres(y.pred = yp, y.ref = y.ref, ncomp.selected = object$ncomp.selected,
xdecomp = xdecomp, ydecomp = ydecomp)
Major fields:
$ncomp.selected - number of selected components
$y.pred - array with predicted y values
$y.ref - matrix with reference y values
$rmse - root mean squared error
$r2 - coefficient of determination
$slope - slope for predicted vs. measured values
$bias - bias for prediction vs. measured values
$ydecomp - decomposition of y values (ldecomp object)
$xdecomp - decomposition of x values (ldecomp object)pls.model.soc$res$cal$xdecomp
Results of data decomposition (class ldecomp).
Major fields:
$scores - matrix with score values
$T2 - matrix with T2 distances
$Q - matrix with Q residuals
$ncomp.selected - selected number of components
$expvar - explained variance for each component
$cumexpvar - cumulative explained variancepls.model.soc$res$test
PLS results (class plsres)
Call:
plsres(y.pred = yp, y.ref = y.ref, ncomp.selected = object$ncomp.selected,
xdecomp = xdecomp, ydecomp = ydecomp)
Major fields:
$ncomp.selected - number of selected components
$y.pred - array with predicted y values
$y.ref - matrix with reference y values
$rmse - root mean squared error
$r2 - coefficient of determination
$slope - slope for predicted vs. measured values
$bias - bias for prediction vs. measured values
$ydecomp - decomposition of y values (ldecomp object)
$xdecomp - decomposition of x values (ldecomp object)pls.model.soc$res$test$xdecomp
Results of data decomposition (class ldecomp).
Major fields:
$scores - matrix with score values
$T2 - matrix with T2 distances
$Q - matrix with Q residuals
$ncomp.selected - selected number of components
$expvar - explained variance for each component
$cumexpvar - cumulative explained varianceLet’s grab the test predictions for a customized plot.
# Grabbing test predictions
test.predictions <- pls.model.soc$res$test$y.pred
dim(test.predictions)[1] 90 20 1# Selecting "Comp 5 predictons"
test.predictions <- tibble(predicted = test.predictions[,5,1])
# Formatting
neospectra.test.results <- neospectra.test %>%
select(-all_of(spectral.column.names)) %>%
bind_cols(test.predictions) %>%
rename(observed = oc_usda.c729_w.pct) %>%
mutate(predicted = expm1(predicted))And calculated additional evalution metrics.
# Calculating performance metrics
library("yardstick")
neospectra.test.performance <- neospectra.test.results %>%
summarise(n = n(),
rmse = rmse_vec(truth = observed, estimate = predicted),
bias = msd_vec(truth = observed, estimate = predicted),
rsq = rsq_trad_vec(truth = observed, estimate = predicted),
ccc = ccc_vec(truth = observed, estimate = predicted, bias = T),
rpiq = rpiq_vec(truth = observed, estimate = predicted))
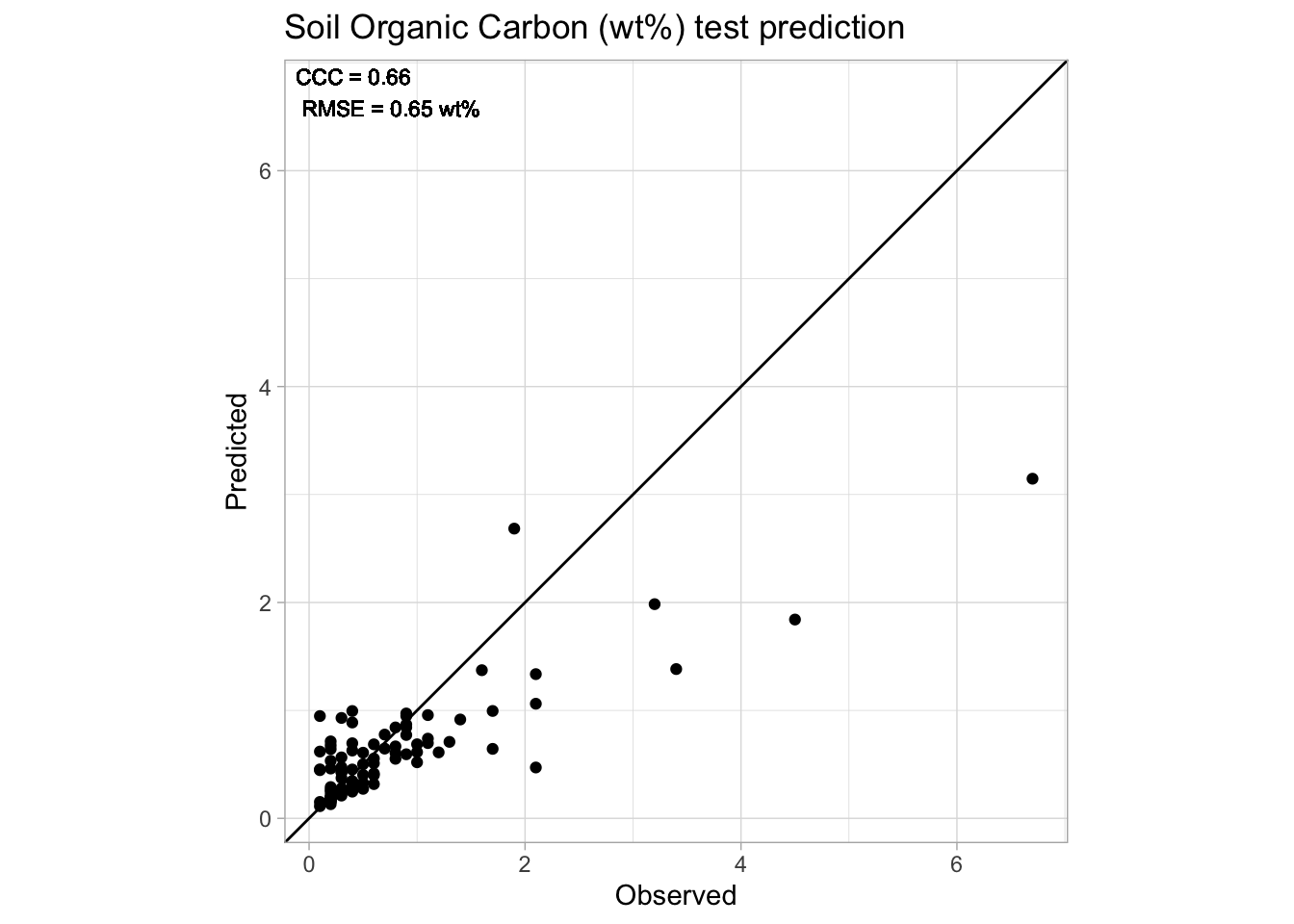
neospectra.test.performance# A tibble: 1 × 6
n rmse bias rsq ccc rpiq
<int> <dbl> <dbl> <dbl> <dbl> <dbl>
1 90 0.646 0.152 0.561 0.658 1.08And plot the scatterplot with ggplot.
# Final accuracy plot
perfomance.annotation <- paste0("CCC = ", round(neospectra.test.performance[[1,"ccc"]], 2),
"\nRMSE = ", round(neospectra.test.performance[[1,"rmse"]], 2), " wt%")
p.final <- ggplot(neospectra.test.results) +
geom_point(aes(x = observed, y = predicted)) +
geom_abline(intercept = 0, slope = 1) +
geom_text(aes(x = -Inf, y = Inf, hjust = -0.1, vjust = 1.2),
label = perfomance.annotation, size = 3) +
labs(title = "Soil Organic Carbon (wt%) test prediction",
x = "Observed", y = "Predicted") +
theme_light() + theme(legend.position = "bottom")
# Making sure it we have a square plot
r.max <- max(layer_scales(p.final)$x$range$range)
r.min <- min(layer_scales(p.final)$x$range$range)
s.max <- max(layer_scales(p.final)$y$range$range)
s.min <- min(layer_scales(p.final)$y$range$range)
t.max <- round(max(r.max,s.max),1)
t.min <- round(min(r.min,s.min),1)
p.final <- p.final + coord_equal(xlim = c(t.min,t.max), ylim = c(t.min,t.max))
p.final